Partícula na caixa unidimensional: A Quântica explicando a cor da cenoura
Compartilhe o artigo:
A exploração e estudo da Mecânica Quântica mudou toda a compreensão humana do Universo e possibilitou que a nossa tecnologia pudesse dar um poderoso salto. O entendimento do efeito Fotoelétrico, do efeito Compton, entre outros, a partir de descrições matemáticas e físicas antes não previstas pela Mecânica Clássica (Newtoniana) - como a famosa equação de Schrödinger -, permitiram que as partículas fundamentais da matéria pudessem ser melhor analisadas e compreendidas, assim como a interação entre essas partículas. Podemos explicar quase tudo com a Quântica, descrevendo e prevendo comportamentos diversos.
No ensino superior, em áreas que envolvem a Química e a Física, um exemplo bem comum para demonstrar a aplicabilidade da Teoria Quântica em fenômenos do dia-a-dia é a sua utilização para prever a cor de pigmentos orgânicos conjugados. Nesse sentido, pode-se mostrar como a cor laranja da cenoura e de outros pigmentos diversos podem ser explicadas pelo modelo da partícula em uma caixa de potencial unidimensional (o mais simples possível).
Esse modelo simples tem sido exaustivamente utilizado em livros didáticos do ensino superior e historicamente empregado com sucesso para explicar a cor de pigmentos cianinas ou outras moléculas conjugadas coloridas com uma relativa pequena cadeia carbônica contendo ligações duplas conjugadas. Porém, tornou-se também comum o emprego didático desse mesmo modelo em grandes cadeias, especialmente na molécula de beta-caroteno (responsável pela cor laranja da cenoura e de outros derivados vegetais). E, nesse ponto, temos um erro frequentemente ignorado e que pode acabar confundindo o estudante, porque se para cadeias pequenas os valores teóricos calculados e aqueles obtidos experimentalmente são bem próximos, para grandes cadeias conjugadas tal aproximação torna-se impossível, a não ser que outros parâmetros adicionais sejam utilizados para compensar a simplicidade do modelo.
Neste artigo, será demonstrado como funciona o modelo da partícula em uma caixa de potencial unidimensional e o porquê ele falha tanto quando aplicado em moléculas com cadeias conjugadas muito grandes, caso um tratamento mais sofisticado não seja levado em conta.
- Continua após o anúncio -
CORES NA NATUREZA
Embora a teoria quântica na matemática seja primorosa, ela de nada vale se não encontrar aplicação e concordância com a prática. Ora, o papel da teoria, no meio acadêmico, é justamente esse: explicar fenômenos práticos, naturais. Assim como a Mecânica Relativística primeiro desenvolvida por Einstein conseguiu melhor descrever a gravidade em comparação com a Mecânica Clássica, a Mecânica Quântica, apoiada principalmente pela equação desenvolvida por Erwin Schrödinger, veio para melhor descrever o universo atômico.
Em patamares bem simples, os frutos da equação de Schrödinger nos deram a solução de problemas unidimensionais, como a movimentação de partículas delimitadas por barreiras de potencial. E temos aplicações práticas relativamente satisfatórias, como a absorção de determinados comprimentos de luz por moléculas com ligações conjugadas. Exemplificando, podemos aplicar a equação da energia total associada com o 'pulo quântico' em moléculas de pigmentos. Analisando as estruturas dessas moléculas, podemos trazê-las como um modelo razoavelmente bom de uma caixa de potencial. Mas existe um grande porém nessa história.
Antes de tudo, vamos explicar como as cores dos objetos ao nosso redor são formadas - um fenômeno quântico. A luz branca do Sol, por exemplo, é composta por vários comprimentos de onda, com cada um deles representando uma faixa do espectro eletromagnético. O espectro eletromagnético reúne todas as radiações eletromagnéticas (compostas por uma partícula-onda chamada 'fóton') e quanto menor o comprimento de onda associado, maior é a energia. Nossa visão consegue perceber comprimentos de onda que variam de ~400 até ~750 nanômetros, ou seja, o intervalo do espectro eletromagnético chamado de 'visível'. Todas as faixas com comprimentos de onda maiores ou menores não podem ser percebidos pela nossa visão, mas podem interagir com o nosso corpo de outras formas, como as perigosas radiações gama, raios-X e ultravioleta, e as mais inofensivas radiações no infravermelho e no rádio.
Na manifestação de cor nos objetos ao nosso redor iluminados pelo Sol, primeiro temos a incidência da luz solar e, enquanto alguns comprimentos são absorvidos pelos elétrons presentes na superfície desses objetos, outros são refletidos. Os comprimentos absorvidos podem aquecer o objeto - transformação da energia absorvida em cinética - e reemitir outros fótons com um maior comprimento de onda do original (efeito Compton), mas obviamente com um considerável atraso. Dependendo da mistura dos comprimentos de onda na faixa do visível refletidos de imediato (não absorvidos), uma cor será formada como resultado final. Nos extremos, teríamos os objetos brancos e os pretos. Nos objetos brancos, todos os comprimentos visíveis são idealmente refletidos. Já nos objetos pretos, todos os comprimentos visíveis são idealmente absorvidos. No caso da cor branca, podemos comprovar facilmente que ela é a mistura de todas as cores fazendo girar rapidamente um Disco de Newton, este o qual é um disco que contém todas as faixas representativas das cores, como mostrado na figura abaixo (um disco mais simples). .
-------------
> Um fato interessante é perceber que os objetos pretos se aquecem muito mais rapidamente quando atingidos pela luz solar do que objetos brancos. Isso é explicado pelo fato da superfície preta/escura absorver muito mais faixas de comprimentos de onda, com cada um desses últimos associados a uma frequência/energia; ou seja, objetos com cor preta absorvem mais energia devido à assimilação de mais fótons na faixa do visível, e, consequentemente, mais calor é gerado quando a energia cinética dos fótons é transformada em vibração e rotação nas partículas constituintes da superfície incidente.
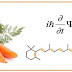
Considerando uma única molécula de um pigmento cianina, este o qual representa um grande espectro de corantes bastante conhecidos que apresentam cores diversas, um elétron absorverá energia vinda da luz solar e pulará para um orbital de maior energia. No caso, um elétron absorverá um comprimento de onda da luz incidente no orbital HOMO, ficará excitado e passará a ocupar o LUMO. A quantidade de energia exata requerida para isso ocorrer dependerá de vários fatores na molécula, indo do grau de ressonância estabilizando a conjugação até os grupos orgânicos ali presentes. Mas podemos fazer belas previsões aproximadas das energias envolvidas ao utilizar modelos quânticos bem simples.
Primeiro de tudo, precisamos usar um modelo quântico que comporte as moléculas de cianina. Se considerarmos que a cadeia carbônica conjugada é plausível de ser representada em termos unidimensionais, podemos encaixá-la na solução do problema de Schrödinger par o modelo de uma partícula em uma caixa unidimensional. Essa caixa é o clássico poço de potencial, onde dentro dele temos uma partícula aprisionada ente duas barreiras infinitas de potencial - por não ter energia suficiente para sair - e submetida a um potencial nulo. E isso fica quase perfeito para a nossa cadeia carbônica, a qual pode ser considerada uma caixa de comprimento indo de 0 até L (como mostrado no esquema abaixo). Os elétrons pi dessa cadeia em ressonância podem se movimentar a vontade de uma lado para o outro nela, com um alto grau de liberdade. Porém, eles só podem fazer isso até os extremos de ligação da cadeia, configurando uma boa aproximação com a caixa de potencial, caso possamos fazer algumas considerações (ignorando solventes e energias muito altas que podem arrancar esses elétrons da molécula, por exemplo).
Sabendo a resolução dessa caixa, e aplicando-a na distribuição energética dos orbitais, basta agora substituirmos os valores exigidos na equação e modificarmos ela para comportar a diferença energética entre os orbitais HOMO e LUMO. Neste ponto, é crucial também sabermos o comprimento L dessa caixa. A partir de valores experimentais encontrados em Handbooks de Química, as ligações em um sistema conjugado - em ressonância - terão valor médio em torno de 0,144 nanômetros. Sabendo que o ângulo formado por três carbonos consecutivos é de 120° (vamos generalizá-lo para toda a cadeia), e utilizando relações simples de trigonometria, fica fácil encontrar o comprimento X da base de cada um dos triângulos e, consequentemente, o comprimento total da caixa, como mostrado no esquema abaixo. Calculando X, obtemos 0,249 nm.
Usando esses valores - variantes para cada molécula de cianina de acordo com o tamanho da cadeia carbônica conjugada - no modelo quântico da caixa de potencial, podemos calcular os comprimentos de onda máximos absorvidos por cada uma das quatro moléculas simétricas de cianina mostradas anteriormente. Para aproximarmos ainda mais os valores calculados dos experimentais (corantes, no caso, dissolvidos em um solvente orgânico, como o etanol), podemos usar um comprimento de 0,567 nm para comportar os grupos nitrogenados entre a delimitação 0,500 e 0,600 nm previamente proposta. Nesse sentido, obtemos excelentes resultados, utilizando de forma mais crua e acessível possível o modelo quântico escolhido.
BETA-CAROTENO
Apesar de termos mostrado que o modelo quântico unidimensional da caixa de potencial funciona bem para explicar as cores observadas de pigmentos orgânicos conjugados possuindo pequenas cadeias carbônicas, isso muda drasticamente à medida que as cadeias conjugadas aumentam. Isso ocorre porque o número crescente de conjugações altera significativamente as energias envolvidas entre o LUMO e o HOMO, passando a não ser mais minimamente comportado pelo modelo ultra-simplificado da caixa de potencial, este o qual não considera uma absorção limitada à faixa de comprimento de onda no visível para um comprimento tendendo ao infinito da cadeia conjugada.
Isso é até óbvio de uma certa perspectiva. Ora, quanto mais conjugações, maior será o tamanho da caixa. Se jogarmos comprimentos de L cada vez maiores na fórmula (solução de Schrödinger para o problema), e tendendo ao infinito, veremos que os valores de absorção tenderão a aumentar para além do infravermelho, fugindo bastante do espectro visível esperado na prática. E os erros consideráveis já começam em moléculas como a luteína, licopeno e, a mais utilizada como exemplo, o beta-caroteno. Geralmente, quando exercícios de Quântica pedem ao estudante de ensino superior para calcular a energia de absorção do beta-caroteno, é dado um valor já pré-estabelecido de comprimento da caixa para a molécula ou, em alguns caso, é pedido ao estudante para calculá-lo via geometria molecular (algo mais errado ainda). Nisso, ocorrem duas coisas: ou o estudante fica perdido sem saber de onde o valor dado foi retirado ou fica doido porque nos cálculos via geometria molecular (ou mesmo através do comprimento linear total das ligações duplas e simples) o resultado final dá uma absorção bem além do infravermelho. Note também que, mesmo o licopeno e o beta-caroteno possuindo uma cadeia conjugada de mesmo tamanho (com 11 ligações duplas conjugadas), a cor final refletida é diferente entre os dois pigmentos, por causa dos diferentes grupos substituintes nas moléculas.
Bem, vamos então demonstrar essa confusão, calculando passo a passo o comprimento de absorção do beta-caroteno a partir de um valor de comprimento de caixa/cadeia conjugada frequentemente dado de antemão pelos livros didáticos (o qual pode variar bastante): 1,83 nm - ou 18,3Å (ångström), unidade mais comumente utilizada para representar distâncias a nível atômico e molecular. O HOMO do betacaroteno está no orbital 11 e sua transição energética durante a absorção de luz será para o orbital 12 ao absorver um fóton.
No final, obtemos um resultado que se aproxima daquele observado na prática experimental, ou seja, de 453 nm. Seria algo até louvável considerando o tamanho da cadeia e um modelo tão simples quanto a caixa de potencial, porém, esse valor de 0,183 nm é apenas um valor aleatoriamente escolhido para melhor se encaixar com o modelo quântico, o que torna todo o processo frustrante para o estudante. Por isso esse comprimento fornecido varia tanto de livro para livro. Na verdade, é necessário utilizar significativos parâmetros de correção para conseguir usar razoavelmente bem a caixa de potencial para moléculas como o beta-caroteno. Se fôssemos usar a mesma lógica simples utilizada para a cianina, o comprimento da caixa comportando o beta-caroteno seria de, no mínimo, 2,615 nm - ou 26,15 Å -, ou seja, representando 10,5 triângulos isósceles. Nesse caso, obteríamos o valor de absorção máxima em 1029,94 nm. Esse valor encontra-se já bem dentro do infravermelho, e se afasta bastante do valor esperado (453 nm).
CONCLUSÃO
Enquanto é mais do que válido demonstrar a grande aplicabilidade e utilidade dos modelos quânticos em fenômenos que não se limitam a campos tecnológicos mais complexos ou abstratos para o estudante, é preciso planejar bem os exercícios de demonstração para não confundir o aluno. Em especial, o modelo da caixa de potencial para explicar a cor laranja da cenoura não é um bom exemplo nesse sentido. Seria uma melhor ideia trabalhar com os alunos o porquê desse modelo simples não funcionar bem para moléculas de pigmentos com cadeias conjugadas muito grandes do que jogar números aleatórios para o comprimento da caixa que melhor se ajustam aos valores esperados, apenas visando forçar a demonstração de um exemplo cotidiano muito comum (já que praticamente todo mundo conhece muito bem uma cenoura, diferente de corantes como a cianina).
Artigos Recomendados:
REFERÊNCIAS CIENTÍFICAS
-------------
No disco de Newton, também podemos perceber uma relação muito interessante. A cor de absorção máxima de um objeto relaciona-se com a sua cor final percebida pela nossa visão: ela será o oposto da cor do objeto no disco de Newton. Por exemplo, o pigmento de cor da cenoura, o beta-caroteno, absorve um máximo em 453 nm, ou seja, no comprimento de onda da cor azul. E qual o oposto/complemento da cor azul no disco? Sim, o laranja! O pigmento principal do tomate é o licopeno e a sua absorção máxima se dá em 472 nm, ou seja, próximo já do verde. A cor emitida acaba sendo o vermelho, algo razoavelmente de acordo com o disco, já que o vermelho e o laranja se encontram próximos (lembrando que o disco não é uma regra absoluta, apenas uma relativa boa aproximação, e outros fatores também contam; além disso, os intervalos de comprimento de onda para cada cor é aproximado e onde não existe um limite bem definido no começo de uma e fim da outra na observação prática).
Agora podemos entrar nos pigmentos orgânicos conjugados. Na natureza, grande parte dos seres vivos possuem pigmentos nos seus corpos responsáveis pelas cores diversas percebidas. No ser humano, o principal seria a melanina (um grupo de pigmentos responsável pela cor da nossa pele e cabelos), e, nas plantas, a clorofila (responsável pela cor verde na maioria delas). Entre os pigmentos na natureza, muitos deles são compostos orgânicos conjugados, ou seja, representados por moléculas orgânicas (baseadas em carbono) que apresentam ligações duplas intercaladas com ligações simples. Ambos os tipos de ligação são interações covalentes entre os átomos, mas com diferentes forças de ligação e de forma ressonante.
Esses pigmentos geralmente possuem relativas longas cadeias de conjugação entre os átomos de carbono e, na hora da incidência da luz, o comprimento de onda envolvido na absorção estará relacionado com a excitação dos elétrons do orbital HOMO (orbital de mais alta energia preenchido) para o orbital LUMO (orbital de mais baixa energia desocupado), e tenderá a envolver a faixa do visível por causa da menor energia requerida do que o normal devido à ressonância. Esses orbitais são formados pelo preenchimento com elétrons pi das ligações duplas, ou seja, um par para cada uma dessas ligações, sendo o outro par de uma ligação sigma. Na ressonância, esses elétrons pi estão relativamente livres para percorrer um lado a outro da cadeia conjugada, por estarem fracamente ligados em relação aos elétrons sigma.
Agora podemos entrar nos pigmentos orgânicos conjugados. Na natureza, grande parte dos seres vivos possuem pigmentos nos seus corpos responsáveis pelas cores diversas percebidas. No ser humano, o principal seria a melanina (um grupo de pigmentos responsável pela cor da nossa pele e cabelos), e, nas plantas, a clorofila (responsável pela cor verde na maioria delas). Entre os pigmentos na natureza, muitos deles são compostos orgânicos conjugados, ou seja, representados por moléculas orgânicas (baseadas em carbono) que apresentam ligações duplas intercaladas com ligações simples. Ambos os tipos de ligação são interações covalentes entre os átomos, mas com diferentes forças de ligação e de forma ressonante.
Esses pigmentos geralmente possuem relativas longas cadeias de conjugação entre os átomos de carbono e, na hora da incidência da luz, o comprimento de onda envolvido na absorção estará relacionado com a excitação dos elétrons do orbital HOMO (orbital de mais alta energia preenchido) para o orbital LUMO (orbital de mais baixa energia desocupado), e tenderá a envolver a faixa do visível por causa da menor energia requerida do que o normal devido à ressonância. Esses orbitais são formados pelo preenchimento com elétrons pi das ligações duplas, ou seja, um par para cada uma dessas ligações, sendo o outro par de uma ligação sigma. Na ressonância, esses elétrons pi estão relativamente livres para percorrer um lado a outro da cadeia conjugada, por estarem fracamente ligados em relação aos elétrons sigma.
-----------
> Moléculas orgânicas insaturadas são aquelas que apresentam ligações duplas ou triplas na sua estrutura. Em cada ligação dupla, existe uma ligação sigma (σ) e uma ligação pi (π), e, em cada ligação tripla, temos duas ligações π e uma ligação σ. Cada ligação π ou σ traz um par de elétrons.
Considerando uma única molécula de um pigmento cianina, este o qual representa um grande espectro de corantes bastante conhecidos que apresentam cores diversas, um elétron absorverá energia vinda da luz solar e pulará para um orbital de maior energia. No caso, um elétron absorverá um comprimento de onda da luz incidente no orbital HOMO, ficará excitado e passará a ocupar o LUMO. A quantidade de energia exata requerida para isso ocorrer dependerá de vários fatores na molécula, indo do grau de ressonância estabilizando a conjugação até os grupos orgânicos ali presentes. Mas podemos fazer belas previsões aproximadas das energias envolvidas ao utilizar modelos quânticos bem simples.
Sabendo a resolução dessa caixa, e aplicando-a na distribuição energética dos orbitais, basta agora substituirmos os valores exigidos na equação e modificarmos ela para comportar a diferença energética entre os orbitais HOMO e LUMO. Neste ponto, é crucial também sabermos o comprimento L dessa caixa. A partir de valores experimentais encontrados em Handbooks de Química, as ligações em um sistema conjugado - em ressonância - terão valor médio em torno de 0,144 nanômetros. Sabendo que o ângulo formado por três carbonos consecutivos é de 120° (vamos generalizá-lo para toda a cadeia), e utilizando relações simples de trigonometria, fica fácil encontrar o comprimento X da base de cada um dos triângulos e, consequentemente, o comprimento total da caixa, como mostrado no esquema abaixo. Calculando X, obtemos 0,249 nm.
- Continua após o anúncio -
BETA-CAROTENO
Apesar de termos mostrado que o modelo quântico unidimensional da caixa de potencial funciona bem para explicar as cores observadas de pigmentos orgânicos conjugados possuindo pequenas cadeias carbônicas, isso muda drasticamente à medida que as cadeias conjugadas aumentam. Isso ocorre porque o número crescente de conjugações altera significativamente as energias envolvidas entre o LUMO e o HOMO, passando a não ser mais minimamente comportado pelo modelo ultra-simplificado da caixa de potencial, este o qual não considera uma absorção limitada à faixa de comprimento de onda no visível para um comprimento tendendo ao infinito da cadeia conjugada.
Isso é até óbvio de uma certa perspectiva. Ora, quanto mais conjugações, maior será o tamanho da caixa. Se jogarmos comprimentos de L cada vez maiores na fórmula (solução de Schrödinger para o problema), e tendendo ao infinito, veremos que os valores de absorção tenderão a aumentar para além do infravermelho, fugindo bastante do espectro visível esperado na prática. E os erros consideráveis já começam em moléculas como a luteína, licopeno e, a mais utilizada como exemplo, o beta-caroteno. Geralmente, quando exercícios de Quântica pedem ao estudante de ensino superior para calcular a energia de absorção do beta-caroteno, é dado um valor já pré-estabelecido de comprimento da caixa para a molécula ou, em alguns caso, é pedido ao estudante para calculá-lo via geometria molecular (algo mais errado ainda). Nisso, ocorrem duas coisas: ou o estudante fica perdido sem saber de onde o valor dado foi retirado ou fica doido porque nos cálculos via geometria molecular (ou mesmo através do comprimento linear total das ligações duplas e simples) o resultado final dá uma absorção bem além do infravermelho. Note também que, mesmo o licopeno e o beta-caroteno possuindo uma cadeia conjugada de mesmo tamanho (com 11 ligações duplas conjugadas), a cor final refletida é diferente entre os dois pigmentos, por causa dos diferentes grupos substituintes nas moléculas.
Bem, vamos então demonstrar essa confusão, calculando passo a passo o comprimento de absorção do beta-caroteno a partir de um valor de comprimento de caixa/cadeia conjugada frequentemente dado de antemão pelos livros didáticos (o qual pode variar bastante): 1,83 nm - ou 18,3Å (ångström), unidade mais comumente utilizada para representar distâncias a nível atômico e molecular. O HOMO do betacaroteno está no orbital 11 e sua transição energética durante a absorção de luz será para o orbital 12 ao absorver um fóton.
- Continua após o anúncio -
CONCLUSÃO
Enquanto é mais do que válido demonstrar a grande aplicabilidade e utilidade dos modelos quânticos em fenômenos que não se limitam a campos tecnológicos mais complexos ou abstratos para o estudante, é preciso planejar bem os exercícios de demonstração para não confundir o aluno. Em especial, o modelo da caixa de potencial para explicar a cor laranja da cenoura não é um bom exemplo nesse sentido. Seria uma melhor ideia trabalhar com os alunos o porquê desse modelo simples não funcionar bem para moléculas de pigmentos com cadeias conjugadas muito grandes do que jogar números aleatórios para o comprimento da caixa que melhor se ajustam aos valores esperados, apenas visando forçar a demonstração de um exemplo cotidiano muito comum (já que praticamente todo mundo conhece muito bem uma cenoura, diferente de corantes como a cianina).
Artigos Recomendados:
- O misterioso Gato de Schrödinger
- Qual a relação entre Ouro, Mercúrio e Relatividade?
- O que é uma Bomba de Hidrogênio?
- Erros mais comuns sobre a Lua
- Por que o calor vai do quente para o frio?
- O que é a Expansão do Universo?
- Por que o céu à noite é escuro?
- Morte Térmica do Universo
REFERÊNCIAS CIENTÍFICAS
- Física Moderna – P. Tipler e R. Llewellyn Ed. LTC
- Física (Vol. 4) – D. Halliday, R. Resnick e K. S. Krane
- https://www.chem.purdue.edu/docs/exams/2012/Crib_January_14_2012.pdf
- https://www.dartmouth.edu/~chemlab/chem6/dyes/full_text/chemistry.html
- http://chemistry.illinoisstate.edu/standard/che362/handouts/362-PinBox-apps1.pdf
- http://www.bu.edu/quantum/notes/QuantumMechanics/ParticleInABox.pdf
- http://article.sapub.org/10.5923.j.jlce.20150302.01.html
- http://faculty.washington.edu/gdrobny/HWS453_2_12.pdf
- http://www.physics.umd.edu/courses/Phys270/Jenkins/LectureChapters41v3.pdf
- https://web.nmsu.edu/~snsm/classes/chem435/Lab5/
- https://notendur.hi.is/hj/EE5/FarrellJCE85.pdf
- http://homepages.gac.edu/~anienow/CHE-372/Labs/Example.pdf
- Fundamentals of Quantum Mechanics - J.E. House, 3°Ed.
